Console Mandelbrot in FORTH

I really like to play around with FORTH. It's a "weird" programming language compared to all the other ones I've learned over time. There are already many articles out there about why you should give it a try, the best probably being this one at Hackaday.

One little program that is often demonstrate on old computers is a BASIC program to compute the Mandelbrot Set in the console. I thought I'd try my hand in "converting" the program to FORTH.

Here's my version, taken from a gist I wrote earlier this year.

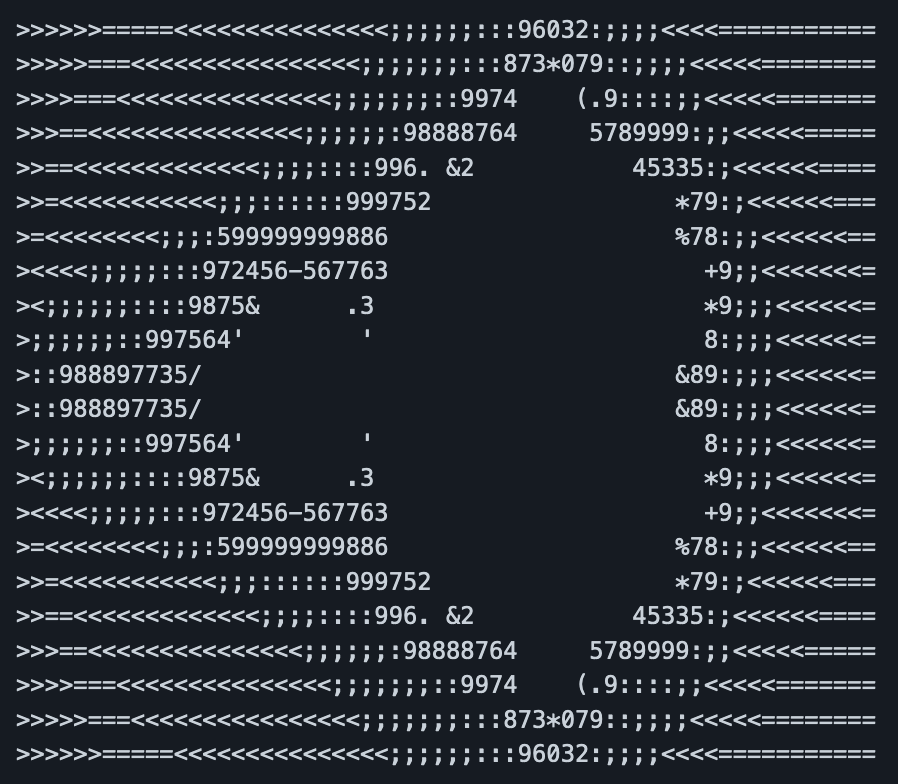
\ from proposal http://www.forth200x.org/fvalue.htmlvariable %var: to 1 %var ! ;: fvalue create f, does> %var @ if f! else f@ then 0 %var ! ;0e0 fvalue i30e0 fvalue r359 value x121 value y1-1e0 fvalue i1 1e0 fvalue i2-2e0 fvalue r11e0 fvalue r2r2 r1 f- x1 s>f f/ fvalue s1 \ L30i2 i1 f- y1 s>f f/ fvalue s2 \ L310e0 fvalue a0e0 fvalue b: single_iter { F: z1 F: z2 } ( F: z1 F: z2 -- F: z1' F: z2' F: mag )  z1 fdup f* to a \ L90  z2 fdup f* to b \ L91  a b f- r3  f+ \ z1 \ L111  2e0 z1 z2 f* f* i3 f+ \ z2 L110  a b f+ \ mag \ line 100;: print_char ( F: x F: y -- )  30 \ push the max in case we don't exit early  30 0 do                          \ L80    single_iter    4e0 f> if drop i leave then  loop                             \ L120  fdrop fdrop \ clean z1 and z2  62 swap - emit                   \ L130;: calc_i3 { y }  i1 s2 y s>f f* f+ to i3 \ L50;: calc_r3 { x }  r1 s1 x s>f f* f+ to r3 \ L70;: mandelcr \ always start on a fresh clean liney1 0 do                         \ L40  i calc_i3  x1 0 do                       \ L60    i calc_r3    r3 i3 print_char  loop                            \ L140  cr                              \ L150loop                              \ L160;mandel

That prints out something like the screenshot at the top of this post.

The "L##" comments roughly refer to the lines in the BASIC version, if you'd like to compare the two. I tried to keep the memory usage and general complexity as equal as possible - that's why there are so many value and fvalue variables. I've seen some examples that use the stack more but are harder to read and have to recompute a lot of things that the BASIC version doesn't.

Here's the original BASIC version:

10 x1=5911 y1=2120 i1=-1.021 i2=1.022 r1=-2.023 r2=1.030 s1=(r2-r1)/x131 s2=(i2-i1)/y140 for y=0  to y150 i3=i1+s2*y60 for x=0 to x170 r3=r1+s1*x71 z1=r372 z2=i380 for n=0 to 2990 a=z1*z191 b=z2*z2100 if a+b>4.0 goto 130110 z2=2*z1*z2+i3111 z1=a-b+r3120 next n130 print chr$(62-n);140 next x150 print160 next y170 end

I'm consistently intrigued by FORTH, so I'll probably be sharing more programs and thoughts. I wrote a short explanation of the "polyfill" in the first four lines of the FORTH version is actually a great dive into the language's extensibility.